-DISTRIBUCIÓN DE PROBABILIDAD CON VARIABLES ALEATORIAS CONTINUAS
Una variable aleatoria continua es una función X que asigna a cada resultado posible de un experimento un número real. Si X puede asumir cualquier valor en algun intervalo I (el intervalo puede ser acotado o desacotado), se llama una variable aleatoria continua. Si puede asumir solo varios valores distintos, se llama una variable aleatoria discreta.
EJERCICIOS:
1.-La siguiente tabla muestra la distribución del residentes estadounidenses (16 años de edad o mayor) quienes asisten a cualquier colegio durante 1980, ordenada por edad:
| Edad | |||||
| Número en 1980 (millones) | 2.7 | 4.8 | 1.9 | 1.2 | 1.8 |
Trace el histograma de la distribución de probabilidad para X= la edad de un universitario elegido al azar..
Solución
Antes de empezar, un poco de terminología: Las entradas de la última fila son denominadas como las frecuencias y la tabla como una distribución de frecuencias. Al sumar las frecuencias, observamos que el número total de universitarios durante 1980 fue 12.4 millón. Por lo tanto, podemos convertir todos aquellos datos en probabilidades por dividir entre este total.
| Edad | |||||
| Probabilidad |
Las probabilidades en la tabla más arriba han sido redondeadas, con la consecuencia que suman a 1.01 en vez de lo 1 esperado. In la categoría 15-19, hemos incluido todos de la edad al menos 15 años y menor que 20 años. Por ejemplo, alguien de la edad de 19½ sería incluyendo en este rango. Desearíamos en cambio escribir 15-20, pero esto sería ambiguo, pues no sabríamos donde contar alguien de la edad de precisamente 20 años. Sin embargo, la probabilidad de que un universitario este precisamente de la edad de 20 (y no, por ejemplo, 20 años y 1 segundo) es esencialmente cero, entonces no importa esta ambigüedad (vea el análisis después de Ejemplo 2 más abajo). Por lo tanto, reescribimos la tabla con estos rangos:
| Edad | |||||
| Probabilidad |
La tabla nos informa, por ejemplo, que
P(15  X
X 20)=
20)= 22
22
y
P(X  35)=
35)= 15
15
El histograma de la distribución de probabilidad es la gráfica de barras que obtenemos al trazar estos datos:
Antes de seguir... Si hubiera sido más fina la agrupación entre rangos—por ejemplo, con divisiones de 1 año en vez de 5 (y si tuviéramos también los datos anual)—entonces pareciera más pulido el histograma, con barras más bajas como muestra debajo. ¿Porqué?
2.- Sea X una variable aleatoria continua que tiene la siguiente función de densidad:
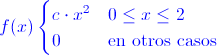
Hallar:
a) El valor de c para que f(x) sea una función de densidad.
Empleamos la expresión de función de densidad de probabilidad:
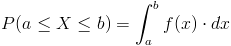
Para los intervalos expuestos en el enunciado del problema, en este caso:
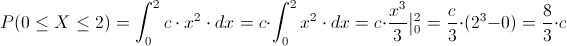
Para que una variable aleatoria continua posea una función de densidad de probabilidad, tienen que cumplirse las siguientes condiciones:
1. f(x) > 0,...para todo x.
2. 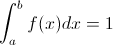
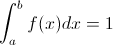
La función f(x) es mayor que cero, por lo que nos queda, satisfacer la primera condición:
(8/3)·c = 1
Y así, obtenemos el valor de c y la solución del problema, para que f(x) sea una función de densidad de probabilidad, el valor de c es de 3/8.
Por lo tanto, la función de densidad de la variable aleatoria continua X queda:
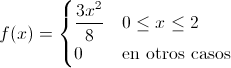
3.- b) Obtener la función de distribución.
Empleamos la expresión de función de distribución acumulada:
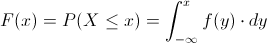
En nuestro caso, el intervalo que tenemos que realizar cálculos es 0 ≤ t ≤ x:
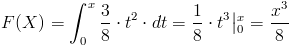
Ya que si x < .0, la función de distribución es 0, y si x > 2, la función de distribución es 1, por lo tanto, la función de distribución acumulada queda tal y como se muestra a continuación:
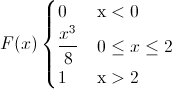
4.- c) Calcular: P(1 ≤ X ≤ 2).
Para calcular dicha probabilidad, empleamos la función de distribución acumulada tal y como se muestra a continuación:
P(1 ≤ X ≤ 2) = F(2) - F(1) = 2³/8 - 1³/8 = 7/8
5.- d) Calcular la esperanza y la varianza de X.
En este apartado, debemos calcular la esperanza y la varianza de la variable aleatoria continua, X.
Para el cálculo de la esperanza, empleamos la siguiente expresión:
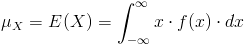
Por lo tanto, la esperanza de X, será:
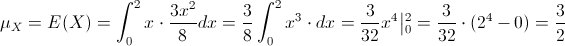
Y para la varianza, se empleará la siguiente expresión:
Var(X) = E(X²) - [E(X)]²
Por lo tanto:
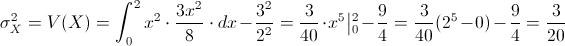
6.- e) Si X es la cantidad diaria vendida de un producto y la ganancia del vendedor es 5 unidades monetarias por cada unidad de producto vendida si X ≤ 1, y 8 unidades monetarias si X > 1, encontrar la ganancia esperada del vendedor para cualquier día especificado.
Para este último apartado, nos dan otra función de la misma variable aleatoria continua X, tal que:
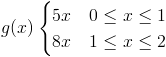
Nos piden la ganancia esperada del vendedor, para obtenerla, usamos la siguiente expresión:
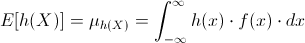
Por lo tanto:
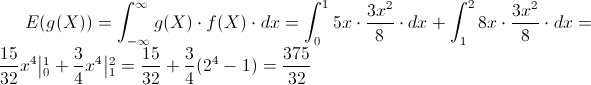
7.- Una prueba consta de 200 preguntas de verdadero o falso, para un sujeto que respondiese al azar, determinar cuál sería la probabilidad de que acertase:
a) 50 preguntas o menos.
Sea la variable aleatoria discreta X,número de aciertos a preguntas dadas. Realizamos un resumen de los datos que nos ofrece el enunciado del problema:
La variable aleatoria discreta X, sigue una distribución binomial: X ~ B(200, 0.5).
Al ser preguntas de verdadero/falso, la probabilidad de acierto es de 0.5.
Comprobaremos, si se puede aproximar a la normal, para ello, se deben cumplir las siguientes condiciones:
1. n·p ≥ 5: 200·0.5 = 100 ≥ 5 OK.
2. n·q ≥ 5: 200·(1-0.5) = 100 ≥ 5 OK.
Como podemos comprobar, cumple las restricciones necesarias, por lo que resolveremos este problema usando la aproximación a la normal:
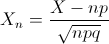
Por lo tanto: X ~ N(n·p, √(n·p·q)) = N(100, √50).
Pasamos a resolver los apartados dados.
solución:
Debemos calcular: P(X ≤ 50), pero antes, debemos aplicar la corrección por continuidad, por lo tanto, tenemos: P(X ≤.50.5).
Tipificamos:
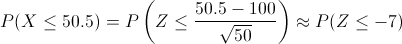
Operamos:
P(X ≤.50.5) ≈ P(Z ≤.-7) = P(Z ≥ 7) = 1 - P(Z ≤.7) = 1 - (0.5 + Φ(7))] = 0.5 - Φ(7)
En las tablas de la Normal tipificada, se dispone del valor exacto en las tablas que están en Aqueronte para su consulta, por lo tanto: Φ(7) = 0.5.
Por lo tanto, la solución a este apartado es la siguiente:
P(X ≤.50.5) ≈ P(Z ≤.-7) = 0.5 - Φ(7) = 0.5 - 0.5 = 0
Se puede concluir con el dato obtenido es que la probabilidad de que un individuo acierte menos o igual a cincuenta preguntas es nula, por lo tanto, se entiende que se acertarán más.
8.- b) Más de 50 y menos de 100.
solución:
Debemos calcular: P(50 < .X < .100), pero antes, debemos aplicar la corrección por continuidad, por lo tanto, tenemos: P(50.5 < .X < .99.5).
Tipificamos:

Simplificamos:
P(50.5 < .X < .99.5) ≈ P(-7 < .Z < .-0.07)
Operamos:
P(50.5 < .X < .99.5) ≈ P(-7 < .Z < .-0.07) = [1 - (0.5 + Φ(0.07))] - [1 - (0.5 + Φ(7))]
Simplificamos:
P(50.5 < .X < .99.5) ≈ P(-7 < .Z < .-0.07) = Φ(7) - Φ(0.07)
En las tablas de la Normal tipificada, se dispone del valor exacto en las tablas que están en Aqueronte para su consulta, por lo tanto:
· Φ(0.07) = 0.0279.
· Φ(7) = 0.5.
Por lo tanto, la solución a este apartado es la siguiente:
P(50.5 < .X < .99.5) ≈ P(-7 < .Z < .-0.07) = Φ(7) - Φ(0.07) = 0.5 - 0.0279 = 0.4721
solución:
Debemos calcular: P(X >.120) = 1 - P(X ≤ 120), pero antes, debemos aplicar la corrección por continuidad, por lo tanto, tenemos: 1 - P(X ≤.120.5).
Tipificamos:
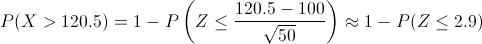
Operamos:
P(X >.120) ≈ 1 - P(Z ≤ 2.9) = 1 - (0.5 + Φ(2.9)) = 0.5 - Φ(2.9)
En las tablas de la Normal tipificada, se dispone del valor exacto en las tablas que están en Aqueronte para su consulta, por lo tanto:
· Φ(2.9) = 0.4981.
Por lo tanto, la solución a este apartado es la siguiente:
P(X >.120) ≈ 1 - P(Z ≤ 2.9) = 0.5 - Φ(2.9) = 0.5 - 0.4981 = 0.0019
Por lo tanto, acertar más de 120 preguntas de un total de 200 es de 0.0019, una probabilidad baja.
10.- Sea X la cantidad de espacio que ocupa un artículo colocado en una caja de empaque de 1 pie cúbico. La función de distribución de probabilidad de X es:
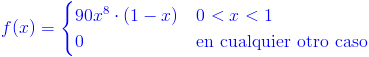
Hallar:
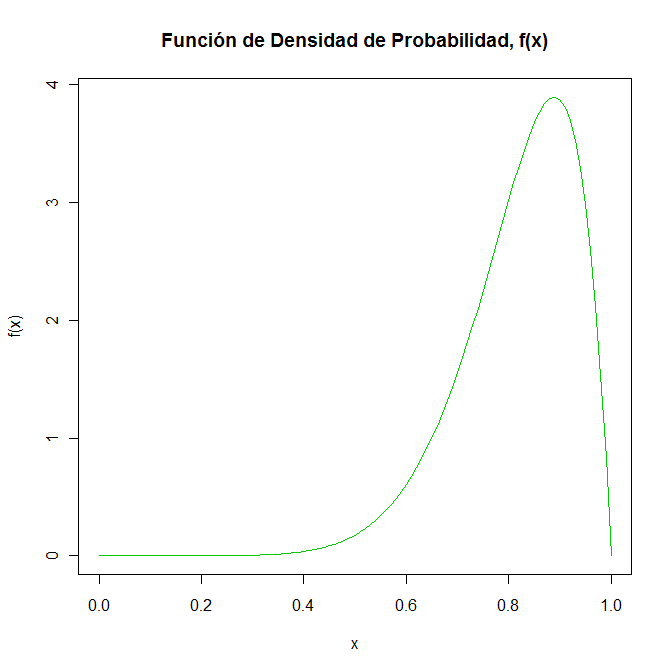
a) Dibuje la función de distribución de probabilidad. Obtenga la función de distribución acumulada y dibújela también.
> x=seq(0,1,by=0.01) #Definimos el rango del eje X con un paso de 0.01
> y=90*(x^8)*(1-x) # Función de densidad de probabilidad en el rango X
Para obtener la función de distribución acumulada, empleamos la siguiente expresión:
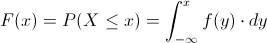
En nuestro caso, el intervalo que tenemos que realizar cálculos es 0 < . X < . 1:
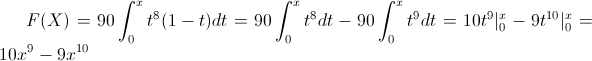
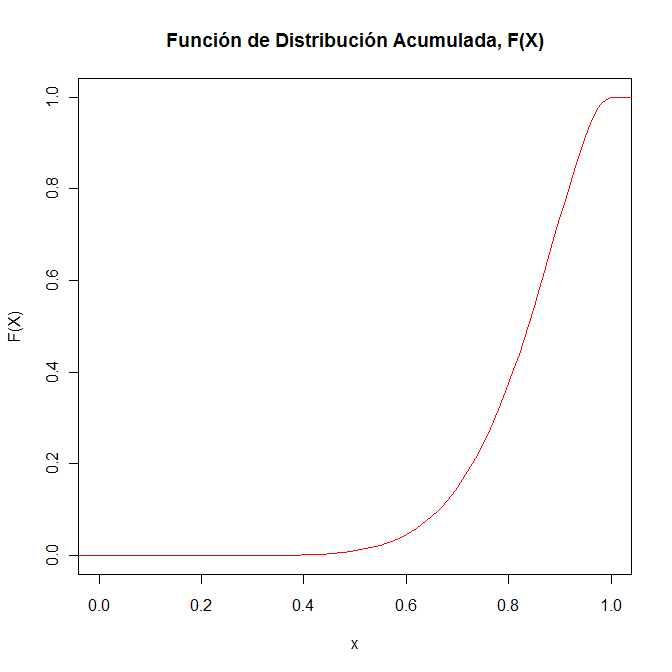
Ya que si x < .0, la función de distribución es 0, y si x > 1, la función de distribución es 1, por lo tanto, la función de distribución acumulada queda tal y como se muestra a continuación:
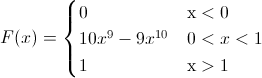
La representación gráfica de la función de distribución acumulada F(X) se muestra en la siguiente figura:
11.- b) Calcular: P(X ≤ 0.5).
Para calcular la probabilidad de este apartado, empleamos la función de distribución acumulada tal y como se muestra a continuación:
P(X ≤ 0.5) = F(0.5) = 10·0.5⁹ - 9·0.5¹⁰ = 11/1024
12.- c) Calcular: P(0.25 ≤ X ≤ 0.5) y P(0.25 < X ≤ 0.5).
En las variables aleatorias continuas, los límites de las probabilidades no se tienen en cuenta, ya que son variables continuas, por lo tanto:
P(0.25 ≤ X ≤ 0.5) = P(0.25 < X ≤ 0.5) = F(0.5) - F(0.25) = [10·0.5⁹ - 9·0.5¹⁰] - [10·0.25⁹ - 9·0.25¹⁰] ≈ 0.0107
13.- d) Obtener el valor medio y la desviación estándar.
En este apartado, debemos calcular la esperanza y la desviación estándar de la variable aleatoria continua, X.
Para el cálculo de la esperanza, empleamos la siguiente expresión:
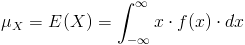
Por lo tanto, la esperanza de X, será:
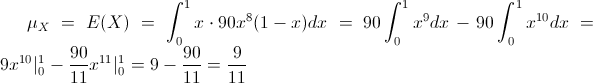
Y para la varianza, se empleará la siguiente expresión:
Var(X) = E(X²) - [E(X)]²
Por lo tanto:
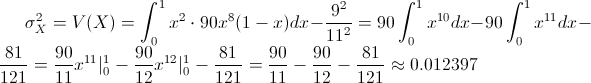
Una vez obtenida la varianza, hallamos la desviación estándar:
σX = √0.012397 ≈ 0.111340
14.- Sea una variable aleatoria continua X que indica el diámetro de un agujero perforado en una hoja de metal. Los datos históricos muestran que la distribución de X puede ser modelado por una función de densidad de probabilidad:
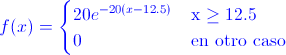
Hallar:
a) Verificar que se trata de una función de densidad de probabilidad válida.
Para que la función f(x) corresponde a una función de densidad de probabilidad de una variable aleatoria continua, se debe cumplir las siguientes condiciones.
1. f(x) > 0,...para todo x.
2. 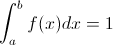
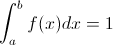
Procedemos:
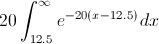
Hacemos un cambio de variable:
· t = -20(x - 12.5)
· dt = -20dx
Aplicamos el cambio de variable:
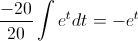
Deshacemos el cambio de variable y resolvemos:
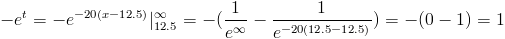
Se cumplen las condiciones por lo que f(x) es una función de densidad de probabilidad legítima de X.
15.- b) Obtener la función de distribución acumulada.
Para obtener la función de distribución acumulada.
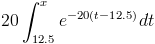
Realizamos un cambio de variable del apartado anterior y resolvemos:
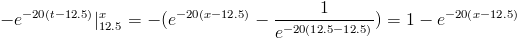
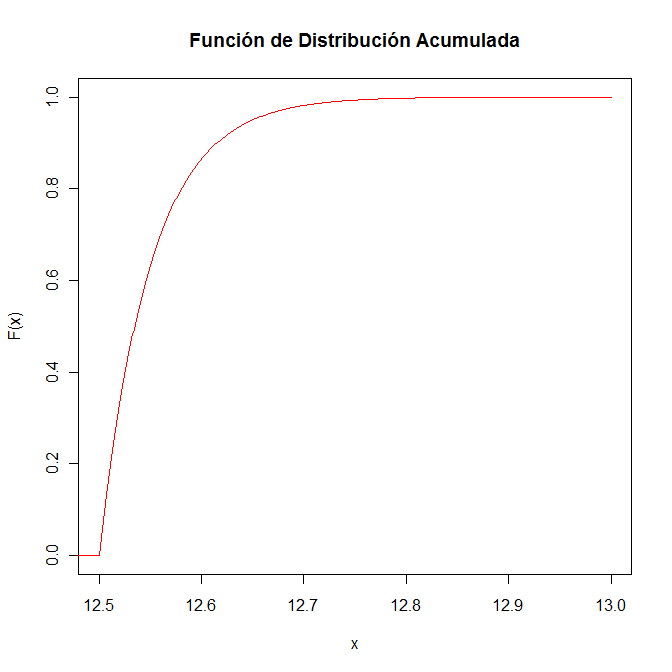
Por lo tanto, la función acumulada quedará:
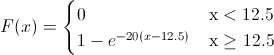
16.- c) Calcular la probabilidad P(12.5 ≤ X ≤ 12.6).
Para obtener la probabilidad requerida, usamos la función de distribución acumulada del apartado anterior.
P(12.5 ≤ X ≤ 12.6) = F(12.6) - F(12.5) = (1 - e-20(12.6-12.5)) - (1 - e-20(12.5-12.5)) = 1 - e-2 ≈ 0.864665
17.- Los ingresos de los ejecutivos junior en una gran empresa están distribuidos normalmente con una desviación estándar de 1200$. Se piensa hacer un recorte de personal, por lo que los empleados que ganan menos de 28000$ serán despedidos.
Si el despido representa al 10% de tales ejecutivos, ¿cuál es el salario medio actual del grupo de ejecutivos junior?
Sea la variable aleatoria X, el salario de los ejecutivos junior.
Los datos que nos ofrecen son los siguientes:
P(X ≤ 28000) = 0.10
Tipificando a la normal, ya que el problema así nos lo indica:
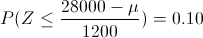
Adaptamos los datos dados a las tablas disponibles en Aqueronte:
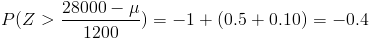
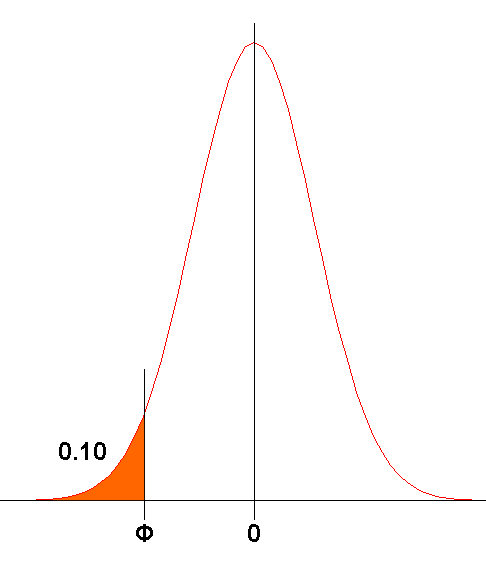
Es negativo ya que la probabilidad se encuentra en el semieje negativo X, gráficamente se ve más claro:
Buscamos en la tabla el valor de -0.40, y en este caso, no se dispone del valor exacto, por lo tanto, interpolamos linealmente:
..-1.28................-Z................-1.29
-0.3997............-0.4.............-0.4015
De donde:
-0.3997 + 0.4015....-> -1.28 + 1.29
-0.3997 + 0.4..-> -1.28 + Z
Calculamos:
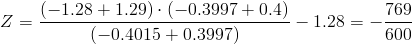
Por lo tanto, ahora disponemos de los datos necesarios para obtener el salario medio actual de los ejecutivos junior:
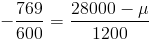
Despejamos el valor medio y obtenemos la solución al problema: μ = 29 538$.
18.- Los ingresos de los ejecutivos junior en una gran empresa están distribuidos normalmente con una desviación estándar de 1200$. Se piensa hacer un recorte de personal, por lo que los empleados que ganan menos de 28000$ serán despedidos.
Si el despido representa al 10% de tales ejecutivos, ¿cuál es el salario medio actual del grupo de ejecutivos junior?
Sea la variable aleatoria X, el salario de los ejecutivos junior.
Los datos que nos ofrecen son los siguientes:
P(X ≤ 28000) = 0.10
Tipificando a la normal, ya que el problema así nos lo indica:
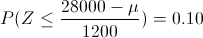
Adaptamos los datos dados a las tablas disponibles en Aqueronte:
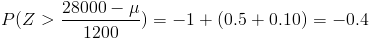
Es negativo ya que la probabilidad se encuentra en el semieje negativo X, gráficamente se ve más claro:
Buscamos en la tabla el valor de -0.40, y en este caso, no se dispone del valor exacto, por lo tanto, interpolamos linealmente:
..-1.28................-Z................-1.29
-0.3997............-0.4.............-0.4015
De donde:
-0.3997 + 0.4015....-> -1.28 + 1.29
-0.3997 + 0.4..-> -1.28 + Z
Calculamos:
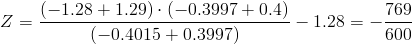
Por lo tanto, ahora disponemos de los datos necesarios para obtener el salario medio actual de los ejecutivos junior:
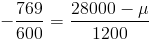



No hay comentarios:
Publicar un comentario