Una variable aleatoria se dice que sigue una distribución normal de media y varianza si su función de densidad se escribe de la forma:
Propiedades:

- Toma valores en todo
.
- Es una función simétrica respecto de
.
- Es estrictamente creciente si
y estrictamente decreciente si
.
- Posee un máximo en
.
- Posee puntos de inflexión en
y
.
- En
posee una asíntota horizontal.
Características:

- Esperanza: La esperanza de la distribución es
.
- Varianza: La varianza de la distribución es
.
- Función Generatriz de Momentos: La función de generatriz de momentos es
- Cambio de origen y escala: La variable no se ve afectada por cambios de origen ni escala, es decir, si
entonces posee la siguiente distribución
EJERCICIOS
4.- Halla las siguientes probabilidades en una distribución N (0,1)
A) P [Z < -1,73]
p[z<-1,73]= p [z>1,73]= 1-p[z<1,73]=1-0.9582 = 0.0418
5.- Halla las siguientes probabilidades en una distribución N (0,1)
B) P[0.62 < Z < 1,34]
p[0.62 < z < 1.34]= p[z< 1.34]-p[z<0.62]= 0.9099-0.7324= 0.1775
6.- Halla las siguientes probabilidades en una distribución N (0,1)
C) P[-1,2 < Z < 1,32]
p[-1.2< z < 1.2]= 2(p[z<1.2]-0.5)= 2(0.8849-0.5)= 0.7698
7.- El tiempo empleado, en horas, en hacer un determinado producto sigue una distribución N(10, 2). Calcula la probabilidad de que ese producto se tarde en hacer:
a) Menos de 7 horas.
p[x<7]=P[x-10/2 < 7-10/2]= p[z<-1.5]= p[z>1.5]= 1-p[z<-1.5]= 1-0.9332= 0.0668
8.- El tiempo empleado, en horas, en hacer un determinado producto sigue una distribución N(10, 2). Calcula la probabilidad de que ese producto se tarde en hacer:
b) Entre 8 y 13 horas.
p[8<x<13]=p[8-10/2<x-10/2<13-10/2]=p[-1<z<1.5] = p[z<1.5]-p[z>1]= p[z<1.5]-(1-p[z<-1])= 0.9332-(1-0.8413)=0.7745
9.- Las ventas diarias, en euros, en un determinado comercio siguen una distribución N(950, 200). Calcula la probabilidad de que las ventas diarias en ese comercio:
a) Superen los 1200 euros.
p[x>12000]=p[x-950/200>1200-950/200]=p[z>1.25]= 1-9[z<-1.25]=1-0.8944=0.1056
10.- Las ventas diarias, en euros, en un determinado comercio siguen una distribución N(950, 200). Calcula la probabilidad de que las ventas diarias en ese comercio:
b) Estén entre 700 y 1000 euros
p[700<x<1000]= p[700-950/200<x-950/200<1000-950/200]=
p[-1<z<0.25]=p[z<0.25]-p[z<-1]=p[z<0.25]-p[z>1]=p[z<0.25]-(1-p[z<-1]= 0.5987-(1-0.8413)=0.44
11.- El nivel de colesterol en una persona adulta sana sigue una distribución normal
N(192, 12). Calcula la probabilidad de que una persona adulta sana tenga un nivel de colesterol:
a) Superior a 200 unidades.
p[x>200]=p[x-192/12>200-192/12]= p[z>0.67]=1-p[z<-0.67]=1-0.7486=0.2514
12.- El nivel de colesterol en una persona adulta sana sigue una distribución normal
N(192, 12). Calcula la probabilidad de que una persona adulta sana tenga un nivel de colesterol:
b) Entre 180 y 220 unidades.
p[180<x<220]=p[180-192/12<x-192/12<220-192/12]=p[-1<z<2.33]=p[z<2.33]-p[z<-1]=p[z<2.33]-p[z>1]=p[z<2.33]-(1-p[z<-1)=0.9901-(1-0.8413)=0.8314
13.- En una distribución normal de media 4 y desviación típica 2, calcular el valor de a para que:
P(4−a ≤ x ≤ 4+a) = 0.5934
P(4−a ≤ x ≤ 4+a) = 0.5934
14.- En una ciudad se estima que la temperatura máxima en el mes de junio sigue una distribución normal, con media 23° y desviación típica 5°. Calcular el número de días del mes en los que se espera alcanzar máximas entre 21° y 27°.
15.- La media de los pesos de 500 estudiantes de un colegio es 70 kg y la desviación típica 3 kg. Suponiendo que los pesos se distribuyen normalmente, hallar cuántos estudiantes pesan: Entre 60 kg y 75 kg.
16.- La media de los pesos de 500 estudiantes de un colegio es 70 kg y la desviación típica 3 kg. Suponiendo que los pesos se distribuyen normalmente, hallar cuántos estudiantes pesan:.Más de 90 kg.
17.- La media de los pesos de 500 estudiantes de un colegio es 70 kg y la desviación típica 3 kg. Suponiendo que los pesos se distribuyen normalmente, hallar cuántos estudiantes pesan:Menos de 64 kg.
18.- de cultura general se observa que las puntuaciones obtenidas siguen una distribución una distribución N(65, 18). Se desea clasificar a los examinados en tres grupos (de baja cultura general, de cultura general aceptable, de excelente cultura general) de modo que hay en el primero un 20% la población, un 65% el segundo y un 15% en el tercero. ¿Cuáles han de ser las puntuaciones que marcan el paso de un grupo al otro?
19.- una de cada tres familias posee teléfono. Si se eligen al azar 90 familias, calcular la probabilidad de que entre ellas haya por lo menos 30 tengan teléfono.







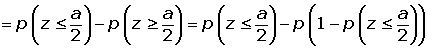






















muy buen
ResponderEliminar